The purpose of a digital signature is to give the receiver of a digital message reason to believe that the message was authored by the person claiming to have sent the message. In addition, digital signatures can be used to provide provable non-repudiation — that is, a digital signature makes it statistically impossible for the author of a signature to simultaneously claim that they didn’t author the message attached to the signature and that the author’s private key is not known by anyone but the author.

To produce and use a digital signature, you need a digital signature scheme.

Definition of a Digital Signature Scheme

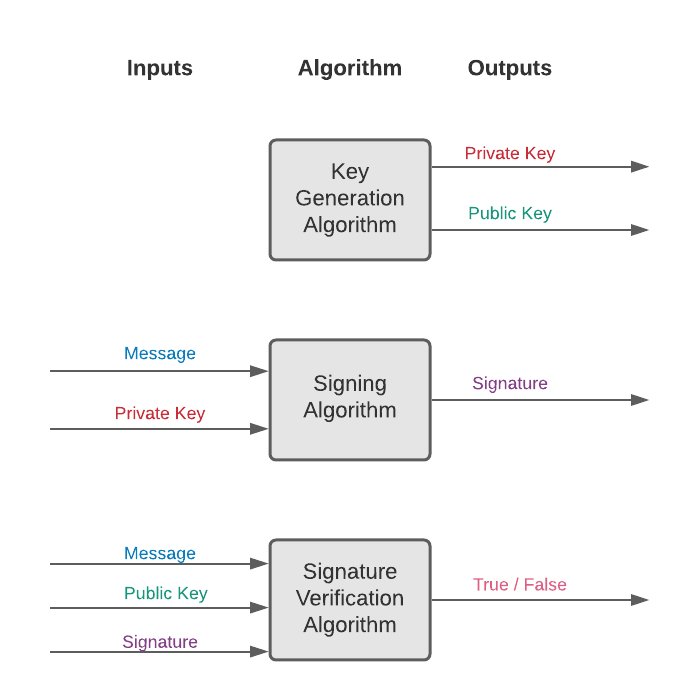
A digital signature scheme consists of three algorithms:

1. A key generation algorithm (“G”). This is a probabilistic algorithm (a probabilistic function) that selects a private key uniformly at random from a set of possible private keys and then returns both the selected private key and the unique public key which corresponds to the selected private key.
2. A signing algorithm (“S”). This is a probabilistic algorithm which takes as input a message (i.e. a binary string) and a private key, and which produces as output a signature.
3. A signature verification algorithm (“V”). This is a deterministic function that takes as input a message, a public key, and a signature, and which returns either ‘true’ or ‘false’. V outputs ‘true’ if the signature was produced by inputting to S (i) the message passed to V and (ii) the private key corresponding to the public key passed to V. Otherwsie, V outputs ‘false’. (In simpler terms, the algorithm V either accepts or rejects a signature’s claim that the owner of the specified public key actually authored the message.)

In practice, for purpose of dealing with variable length messages, digital signature algorithms typically deal with the hash of a message rather than with a message directly. Because of this, there is some nonzero probability that two messages hash to the same message digest, and therefore there is a nonzero probability that the signature verification algorithm will return a false positive.

Complete Example: The Digital Signature Algorithm (DSA)

The Digital Signature Algorithm (DSA) is a standardized digital signature scheme. There are variations of DSA that use different parameters, but for simplicity, we will only consider a single version.

DSA relies on several parameters that are shared by all users of the system:

• H is the cryptographic hash function SHA-256
• L = 3072 is the public key length (in bits)
• N = 256
• q is an arbitrary N-bit prime number
• p is an arbitrary L-bit prime number such that p-1 is a multiple of q
• h is an arbitrary integer from the range {2, … , p-2}. Commonly h=2 is used.
• g = h^(p-1)/q mod p. In the rare case that g = 1, choose a new value for h and try again.

The parameters (H, q, p, g) characterize the version of DSA used and can be shared by everyone.

Key generation algorithm

Each user of the system must use the following key generation algorithm to obtain a private key and a public key:

1. Choose an integer x randomly from {1, … , q-1}
2. Compute y = g^x mod p

x is the private key of the user, and y is the public key of the user. Each user can perform this algorithm on their own and then share their public key with all other users of the system while keeping the private key private.

Signing algorithm

Given a message m (represented in binary and interpreted as a number), it can be signed by the user with private key x as follows:

1. Choose an integer k randomly from {1, … , q-1}
2. Compute r = (g^k mod p) mod q. In the unlikely case that r = 0, start again with a different random k.
3. Compute the message hash d = H(m)
4. Compute j, such that (kj) mod q = 1. j is called the modular inverse of k.
5. Compute the message hash d = H(m)
6. Compute s = ( j(d + xr)) mod q. In the unlikely case that s = 0, start again with a different random k.

The digital signature is the pair (r, s)

Importantly, it is computationally infeasible to create a fake signature without access to x, the private key of the message’s author.

Signature verification algorithm

Anyone can verify that a signature (r, s) is valid for a message m as follows:

1. Verify that 0 < r < q and 0 < s < q
2. Compute w, such that (ws) mod q = 1 (i.e. compute the modular inverse of s)
3. Compute u₁ = (H(m) • w) mod q
4. Compute u₂ = (wr) mod q
5. Compute v = ( g^u₁ y^u₂ mod p) mod q
6. Return ‘true’ (indicating that the signature is valid) if and only if r = v

For more details on the properties of DSA and the different versions of it, you can check out the original patent by an NSA employee or the official, standardized algorithm adopted by the U.S. government, FIPS 186-4.

For those of you interested in crypto, Ethereum uses a modified version of DSA called the Elliptic Curve Digital Signature Algorithm (or ECDSA). The math used by ECDSA is a bit more advanced than the math for standard DSA, but the strength of the security of ECDSA is better by an impressive margin.